The Best Kept Secret of Investing

Compound interest; I bet when you hear that phrase, you’re taken back to a not-so-fond memory of algebra class. Ok, I’ll admit, that part might just be me, but we’ve all heard of that phrase. Or at least, we have some idea of what it is. I mean, it’s a mathematical concept that we’ve known for centuries now. So it’s no secret what compound interest is. Or isn’t it?

There’s an old fable on compound interest that illustrates its power perfectly. The story goes of a man who invents the game of chess and presents it to the king. The king, being very impressed, grants the inventor one wish. The inventor responds to the king with one simple request. He asks the king for a chessboard and to place a grain of wheat on the first square, two on the second, four on the third, and so on. Thinking the inventor has just made a simple request, the king agrees.

The first row of the chessboard costs the king practically nothing. 128 grains of wheat. Not so bad right? Well, things get out of hand pretty quickly after that. By the 21st square, the king owed over a million grains of wheat. By the 41st? 1 trillion grains of wheat. By the time the king figured out what 2⁶⁴th amounted to, he was giving away all the wheat in the entire kingdom!

Actually, It’s even more dramatic than that. By the time you get to the 64th square, the king would have owed 18,446,744,073,709,551,615 (that’s eighteen quintillion) grains of wheat, or 2,000 times the annual world production of wheat. I don’t know about you, but that’s a lot of commas!

So there it is, the true power of compounding illustrated in an old fable. The world knows about it. It’s no secret. Yet, so few people use it. Why has it turned out this way? There may be a few explanations for this.

First, you’ll notice that oftentimes compound interest examples are not presented in the form of dollars. As is in algebra class, it’s presented as something silly like “the number of apples” or with the fable of our not-so-clever king, “grains of wheat” and yet, the math works the excact same way with dollars.

Secondly, our brains are exceptional at thinking about things linearly, not exponentially. It’s a rather difficult concept for our brains to fully grasp.

Good Old Father Time

Ok, I know what you’re thinking. This is great and all, but how on earth do you double your money sixty-four times in one lifetime? Well, I am glad you asked! The answer is, you can’t.

If anyone reading this knows how to double $1 sixty-four times in one life, then I can say unequivocally, that you should be the one writing this article, and I should be the one listening to you!

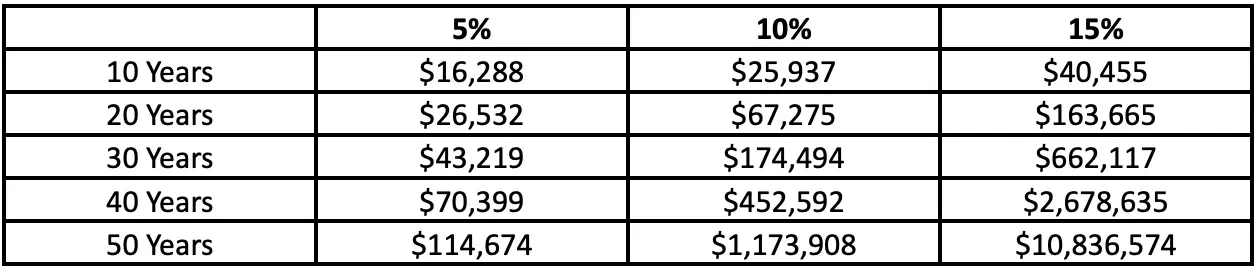
Ok, so if sixty-four doubles is not possible, then what is? Let’s take three different, more realistic scenarios. In the following table, I’ve laid out the compounded value of just $10,000 at 5%, 10%, and 15% for years 10 through 50. I should point out that 15% is not an easy figure to achieve. Statistically, you’re 1 in 1000 if you can achieve that figure over any 10 years.

Have no fear, however! 10% per year is achievable. Not only is 10% per year doable, it’s the average return of the S&P 500.

Im always amazed just by how a small difference in rates of return can change the sum so significantly over a long enough time. Bumping up the investment returns by just 5% in each category can mean a difference of 10x the ending balance. So make no mistake, over an investing lifetime, every percent counts.

But of course, compound interest is not only a function of rate of return, but time as well. The length of your runway is equally as important (if not more) as the rate of return. Let me explain.

The variables of rate and time are interchangeable. So what if we take $10,000 at 15% for 10 years? We get $40,000. Let’s take that same example and flip the numbers. Take $10,000 at 10% for 15 years. Voila! We get $40,000 again. We can overcome the hurdle of lower investment returns by lengthening our runway.

Let’s imagine we’re 21 again, just graduating college, and about to start our careers. And just for fun, let’s pretend that we fully understand the power of compounding. If we manage to save $10,000 the first year, stick it in the S&P 500, and never save another dime until the retirement of 71, we would have $1,173,90. Pretty cool right? Well, It gets even better.

Considering you’re going to get raises as you go, it’s pretty likely you’ll continue saving. So what would happen to that figure if we put away $250 a month after the first $10,000? We end up with $4,238,758! Almost four times the original balance. $500 a month? $7,410,327. $1,000 a month? $13,753,464. Those millions sure do add up pretty quickly!

So what’s the point of all this? Time is your friend in investing. The longer the runway, the better off we are. Start young.

America — A Compounding Machine

In 2018, Warren Buffett took the stage to highlight the concept of compounding to the shareholders of Berkshire Hathaway. Imagine if you had put $10,000 in the S&P 500 back in 1942, the year Warren purchased his first stock. What would that figure be in 2018 if you had reinvested all the dividends?

Before you come up with a number, let’s remind ourselves of all the horrific headlines that have appeared in the world between 1942 and 2018. We had a World War, nuclear invention, countless recessions, crippling inflation in the ’70s, the Cuban Missile Crisis, a Cold War, terrorist attacks, the Financial Crisis of 2008, and countless other awful headlines.

Did I sway your answer?

Well, if you stayed invested through the entire period, it would have amounted to a staggering $51 million by 2018. Roughly 11.8% compounded annually. And that’s just from buying the S&P 500. It doesn’t get much easier than that!

But wait, there’s more! Of course, that was in 2018. A lot has happened since then. We’ve had a once-in-a-century event between then and now. So what if you held that $51 million in the S&P 500 through Covid 19 and now? Surely the world shutting down would have rained on our compounding parade.

Ready for it? Drum roll, please! You would have $85 million today.